| 曲线拟合(1) | 您所在的位置:网站首页 › 增长曲线模型 stata › 曲线拟合(1) |
曲线拟合(1)
|
To be continue … … 文章目录 一、Logistic模型 1.1 Logistic方程概述 1.2 Logistic方程的性质 二、Logistic曲线拟合方法 2.1 Logistic曲线初值的选取 2.2 Logistic曲线的参数拟合方法 2.2.1 三点法 2.2.2 四点法 2.2.3 拐点法 2.2.4 误差估计——决定系数 2.2.5 非线性拟合 三、Logistic预测增长这是创新训练传染病的微分方程模型Logistic曲线笔记 一、Logistic模型Richards曲线拟合方法及初值的选取 1.1 Logistic方程概述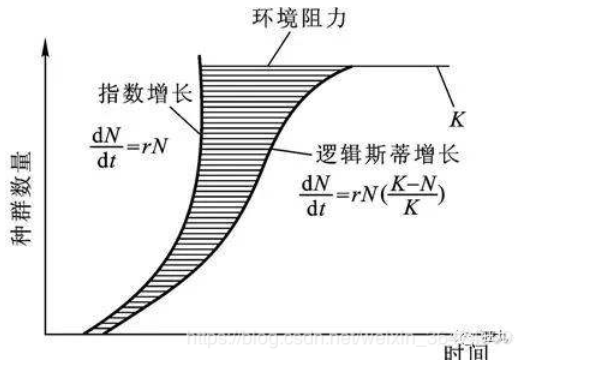 图1
图1
Logistics方程可用下列微分方程描述 { d N d t = r ( 1 − N N m ) N N ( t 0 ) = N 0 (1) \begin{aligned} \begin{cases} \displaystyle \frac{\mathrm{d}N}{\mathrm{d}t}=r\big(1-\frac{N}{N_{m}}\big)N\\ N(t_{0})=N_{0} \end{cases}\tag{1} \end{aligned} ⎩⎨⎧dtdN=r(1−NmN)NN(t0)=N0(1) 变量分离方程,其中 N m N_{m} Nm表示理论上的最大值, N 0 N_{0} N0表示 t 0 t_{0} t0时刻的病人数 分离变量,得 d N ( 1 − N N m ) N N m = r N m d t \frac{\mathrm{d}N}{(1-\frac{N}{N_{m}})\frac{N}{N_{m}}}=rN_{m}\mathrm{d}t (1−NmN)NmNdN=rNmdt 即 1 N d N − 1 N m − N d ( N m − N ) = r d t \frac{1}{N}\mathrm{d}N-\frac{1}{N_{m}-N}\mathrm{d}(N_{m}-N)=r\mathrm{d}t N1dN−Nm−N1d(Nm−N)=rdt 也就是 ln N − ln ( N m − N ) = r t + C ′ ⇒ ln ( N N m − N ) = r t + C ′ ⇒ N N m − N = C e r t ( 其 中 , C = e C ′ ) ⇒ N = N m 1 + 1 / C ⋅ e − r t \begin{aligned} &\ln N-\ln(N_{m}-N)=rt+C'\\ &\Rightarrow \ln(\frac{N}{N_{m}-N})=rt+C'\\ &\Rightarrow \frac{N}{N_{m}-N}=C\mathrm{e}^{rt}(其中,C=\mathrm{e}^{C'})\\ &\Rightarrow N=\frac{N_{m}}{1+1/C\cdot\mathrm{e}^{-rt}} \end{aligned} lnN−ln(Nm−N)=rt+C′⇒ln(Nm−NN)=rt+C′⇒Nm−NN=Cert(其中,C=eC′)⇒N=1+1/C⋅e−rtNm 代入初值条件 N ( t 0 ) = N 0 N(t_{0})=N_{0} N(t0)=N0,得 C = N 0 N m − N 0 e − r t 0 C=\frac{N_{0}}{N_{m}-N_{0}}\mathrm{e}^{-rt_{0}} C=Nm−N0N0e−rt0 代入上式得 N = N m 1 + ( N m N 0 − 1 ) e − r ( t − t 0 ) ⇒ N = 1 1 N m + ( 1 N 0 − 1 N m ) e − r ( t − t 0 ) (2) \begin{aligned} & N=\frac{N_{m}}{1+(\frac{N_{m}}{N_{0}}-1)\mathrm{e}^{-r(t-t_{0})}}\\ & \Rightarrow N=\frac{1}{\frac{1}{N_{m}}+(\frac{1}{N_{0}}-\frac{1}{N_{m}})\mathrm{e}^{-r(t-t_{0})}}\tag{2} \end{aligned} N=1+(N0Nm−1)e−r(t−t0)Nm⇒N=Nm1+(N01−Nm1)e−r(t−t0)1(2) 由上式可看出,令 t → ∞ t\to\infty t→∞, N → N m N\to N_{m} N→Nm,也即 N = N 0 N m e r ( t − t 0 ) N 0 ( e r ( t − t 0 ) − 1 ) + N m N=\frac{N_{0}N_{m}\mathrm{e}^{r(t-t_{0})}}{N_{0}(\mathrm{e}^{r(t-t_{0})}-1)+N_{m}} N=N0(er(t−t0)−1)+NmN0Nmer(t−t0) 另外一种形式的logistic微分方程如下 { d N d t = r N − k N 2 N ( t 0 ) = N 0 (3) \begin{aligned} \begin{cases} \displaystyle \frac{\mathrm{d}N}{\mathrm{d}t}=rN-kN^{2}\\ N(t_{0})=N_{0} \end{cases}\tag{3} \end{aligned} ⎩⎨⎧dtdN=rN−kN2N(t0)=N0(3) 其中, r r r表示发病率, k k k表示预防效果 同理即得 N = 1 k r + ( 1 N 0 − k r ) e − r ( t − t 0 ) N=\frac{1}{\frac{k}{r}+(\frac{1}{N_{0}}-\frac{k}{r})\mathrm{e}^{-r(t-t_{0})}} N=rk+(N01−rk)e−r(t−t0)1 其中, N m = r k , ( w h i l e t → ∞ ) N_{m}=\frac{r}{k},(while\ t\to\infty) Nm |
【本文地址】